jueves, 19 de mayo de 2016
martes, 17 de mayo de 2016
MOVIMIENTO CIRCULAR : MCU Y MCUA
Posición
La posición de la partícula depende de su posición inicial y de la velocidad a la que se desplaza. Ésta se puede calcular a partir del incremento angular, de la velocidad angular y de la velocidad tangencial (en caso de conocer las velocidades es necesario saber el tiempo t que se ha movido el cuerpo o partícula).
Velocidad angular
Otra forma de determinar la velocidad angular es:
Las unidades en las que se mide la velocidad angularω es en radianes/seg, o simplemente en s-1.
En el MCU La velocidad angular ees constante.
Velocidad tangencial
La velocidad tangencial es igual a la velocidad angular por el radio.

La velocidad tangencial, al igual que la velocidad angular, en el MCU es constante.
Aceleración centrípeta
 A diferencia del movimiento rectilíneo uniforme, una partícula en un movimiento circular uniforme (MCU) si que tiene aceleración, la aceleración centrípeta. Esto se debe a que, aunque el módulo de la velocidad se mantiene constante, el vector cambia constantemente de dirección.
A diferencia del movimiento rectilíneo uniforme, una partícula en un movimiento circular uniforme (MCU) si que tiene aceleración, la aceleración centrípeta. Esto se debe a que, aunque el módulo de la velocidad se mantiene constante, el vector cambia constantemente de dirección.
Ésta se calcula como:

Velocidad tangencial
La velocidad tangencial es igual a la velocidad angular por el radio.
Aceleración centrípeta
Ésta se calcula como:
ACELERACIÓN ANGULAR Y TANGENCIAL
En el movimiento circular uniforme (MCU), tanto la aceleración angular como la aceleración tangenciales son cero.
La velocidad angular en el MCU es constante, por lo que el período también será constante e irá definido por la fórmula siguiente:
Frecuencia (f)
La frecuencia es constante al ser constante la velocidad angular y el período:
Ejemplo
Una rueda gira a una velocidad constante de 120 revoluciones por minuto (r.p.m.). Hallar:
- La frecuencia en ciclos/segundo.
- La velocidad angular en radianes/segundo.
- La velocidad tangencial en un punto de la rueda situado a 15 cm. del eje.
- Las aceleraciones tangenciales y centrípetas en el punto citado.
Solución:
- La frecuencia en ciclos/segundo se calcula dividiendo las r.p.m. entre los 60 segundos que tiene un minuto:
- La velocidad angular (ω):
- La velocidad tangencial en un punto de la rueda situado a 15 cm del eje, el radio de rotación será de r=15 cm, por lo tanto:
- La aceleración tangencial es 0:
La aceleración centrípeta en el punto citado es:
El movimiento circular uniformemente acelerado (MCUA) se presenta cuando una partícula o cuerpo sólido describe una trayectoria circular aumentando o disminuyendo la velocidad de forma constante en cada unidad de tiempo.
Es decir, la partícula se mueve con aceleración constante.
En el dibujo se observa un ejemplo en donde la velocidad aumenta linealmente en el tiempo. Suponiendo que el tiempo en llegar del punto P1 a P2 sea una unidad de tiempo, la partícula viaja con una aceleración tangencial uniforme v, incrementándose esa cantidad en cada unidad de tiempo.
Velocidad angular
El sentido de la aceleración angular α puede ser contrario al de la velocidad angular ω. Si la aceleración angular es negativa, seria un caso de movimiento circular uniformemente retardado.
La velocidad tangencial es el producto de la velocidad angular por el radio r.
La velocidad tangencial también se incrementa linealmente mediante la siguiente fórmula:
La velocidad tangencial también se incrementa linealmente mediante la siguiente fórmula:
Dándose aquí igualmente la posibilidad de aceleración negativa que se ha descrito en el apartado anterior.
La aceleración angular en el movimiento circular uniformemente acelerado es constante. Se calcula como el incremento de velocidad angular ω desde el instante inicial hasta el final partido por el tiempo.
Aceleración tangencial
La aceleración tangencial en el movimiento circular uniformemente acelerado MCUA se calcula como el incremento de velocidad v desde el instante inicial hasta el final partido por el tiempo.
Aceleración centrípeta
La aceleración centrípeta en el MCUA se halla mediante:
COMPONENTES INTRÍNSECAS DE LA ACELERACIÓN
La velocidad tangencial por la trayectoria en un punto Pes v. En un intervalo de tiempo pequeño Δt, la velocidad incrementa a v’ en el punto P’, después de haber descrito un ángulo Δφ.
En la figura se puede ver el incremento de la velocidad tangencial Δv descompuesta en dos componentes: la tangencial Δvt y la normal (o centrípeta) Δvn.
Si dividimos ambas componentes de la velocidad por Δt, tendremos las componentes intrínsecas de la aceleración: la aceleración tangencial at y la aceleración normal an (o centrípeta).
 PERÍODO
PERÍODO
En el MCUA la velocidad angular cambia respecto al tiempo.
Por tanto, el períodocada vez será menor o mayor según si decrece o crece la velocidad angular.
Frecuencia
La frecuencia en el caso del MCUA es mayor o menor porque la velocidad angular cambia. La fórmula de la frecuencia será:
| Movimiento de proyectiles | |||||
| Cualquier objeto que sea lanzado en el aire con una velocidad inicial | |||||
Por eso es importante explicar el movimiento de un proyectil como resultado de la superposición de un movimiento rectilíneo uniforme y uno uniformemente variado, estableciendo las ecuaciones de la curva representativa, tiempo de vuelo, tiempo máximo, altura máxima, alcance máximo, velocidad y coordenadas de posición en el plano. | |||||
| ¿Qué es un proyectil? | ||
El movimiento de un proyectil es un ejemplo clásico del movimiento en dos dimensiones con aceleración constante. Un proyectil es cualquier cuerpo que se lanza o proyecta por medio de alguna fuerza y continúa en movimiento por inercia propia. Un proyectil es un objeto sobre el cual la única fuerza que actúa es la aceleración de la gravedad. La gravedad actúa para influenciar el movimiento vertical del proyectil. El movimiento horizontal del proyectil es el resultado de la tendencia de cualquier objeto a permanecer en movimiento a velocidad constante. | ||
| El término proyectil se aplica por ejemplo a una bala disparada por un arma de fuego, a un cohete después de consumir su combustible, a un objeto lanzado desde un avión o en muchas actividades deportivas (golf, tenis, fútbol, béisbol, atletismo etc.). L os fuegos artificiales y las fuentes del agua son ejemplos del movimiento de proyectiles . El camino seguido por un proyectil se denomina trayectoria . El estudio del movimiento de proyectiles es complejo debido a la influencia de la resistencia del aire, la rotación de la Tierra, variación en la aceleración de la gravedad. | ||
La ciencia encargada de hacer el estudio del movimiento de los proyectiles se llama balística. | ||
Experiencia de Galileo Galilei El hombre conocía las trayectorias parabólicas aunque no las denominaba así y experimentaba con tiros parabólicos (Por ejemplo, recuerde las destrezas de David frente a Goliat). Galileo fue el primero que dio una descripción moderna y cualitativa del movimiento de proyectiles dando las bases para su conocimiento y demostró que la trayectoria de cualquier proyectil es una parábola. | ||
| Galileo realizó un experimento con dos objetos: impulsó uno horizontalmente desde una mesa y dejó caer otro cuerpo desde el borde verticalmente. Al dejar caer un cuerpo A verticalmente | ||
El objeto A , en Caída libre tiene solamente la velocidad vertical en un instante t y posee una aceleración que es la de gravedad, luego está dotado de un movimiento uniformemente acelerado. El objeto B está animado en ese instante t de dos movimientos y como consecuencia de dos velocidades perpendiculares: la velocidad vertical de caída y la velocidad horizontal debido al impulso de lanzamiento. | ||
Como los objetos A y B tardan lo mismo en caer, Galileo concluyó que la velocidad horizontal debido al movimiento uniforme, ya que el cuerpo no posee aceleración, no influye en el movimiento de caída del cuerpo B , o sea, que las velocidades | ||
| ||
| Análisis del movimiento de proyectiles | ||
Se examina sólo trayectorias suficientemente cortas para que la fuerza gravitacional se pueda considerar constante en magnitud y dirección. También hay que analizar no tener en cuenta los efectos de la resistencia del aire; Estas hipótesis simplificadas constituyen la base de un modelo idealizado del problema físico. Como, en este caso idealizado, la única fuerza que actúa sobre el proyectil es su peso considerado constante en magnitud y dirección, es mejor referir el movimiento a un sistema de ejes coordenadas rectangulares. Se toma el eje x horizontal y el eje y verticalmente hacia arriba. | ||
| La componente x de la fuerza que actúa sobre el proyectil es nula y la componente y es el peso del proyectil – mg. Esto es, la componente horizontal de la aceleración es nula, y la componente vertical hacia abajo, es igual a la de un cuerpo que cae libremente. Puesto que la aceleración nula significa velocidad constante, el movimiento puede definirse como una combinación de movimiento horizontal con velocidad constante y movimiento vertical con aceleración constante. | ||
| Estos dos movimientos hacen que el movimiento resultante sea de trayectoria parabólica . Dichos movimientos son completamente independientes uno del otro. | ||
| Considérese un proyectil sencillo La componente horizontal del movimiento de un proyectil es igual al movimiento horizontal de una pelota que rueda libremente sobre la superficie plana de la mesa. Si podemos despreciar el efecto de la fricción, la bola se mueve a velocidad constante, recorriendo distancias iguales en intervalos de tiempos iguales. | ||
La componente vertical del movimiento de un proyectil que describe una trayectoria curva es exactamente igual que el movimiento de un objeto en caída libre. El movimiento del proyectil de una pelota que se deja caer, tiene una componente vertical en la dirección de la gravedad terrestre, el proyectil se acelera hacia abajo. El aumento de la rapidez en la dirección vertical hace que el objeto recorra distancias cada vez mayores a intervalos de tiempos iguales. Es interesante notar que la componente horizontal del movimiento de un proyectil es totalmente independiente de la componente vertical. Cada uno de ellas actúa de manera independiente. Sus efectos combinados producen toda la gama de trayectorias curvas que describen los proyectiles. | ||
| Una Fotografía real con luz estroboscópica de dos pelotas de golf que caen simultáneamente, una libremente y la otra que se lanza en forma horizontal revela que el movimiento curvilíneo de la pelota es una combinación de los movimientos horizontal y vertical. | ||
Más consideraciones del Movimiento de ProyectilesConsidérese una bala de cañón que se dispara con determinado ángulo de elevación. Suponga por un momento que no hay gravedad; entonces a causa de la inercia, la bala de cañón seguirá la trayectoria rectilínea representada por la línea discontinua. Pero la gravedad existe, por lo que esto no sucede. Lo que realidad ocurre es que la bala cae continuamente por debajo de la línea imaginaria, hasta que por último llega al suelo. | ||
| Es importante notar que la distancia vertical que un objto cae por debajo de cualquier punto de la línea discontinua es la misma distancia vertical que caería si se soltara desde el reposo en el mismo tiempo. | ||
Si se desprecian los efectos de la resistencia del aire, cualquier objeto que se lanza en este medio describirá una trayectoria parabólica. No obstante en situaciones prácticas la resistencia del aire puede considerarse despreciable sólo en el caso de objetos que se mueven lentamente y que posean altas densidades. Como una roca o una esfera sólida. Los proyectiles de alta-velocidad, como balas de rifles o cañón, son frenados en forma continua por la resistencia del aire y su trayectoria difiere de una parábola. | ||
| La altura vertical y el alcance horizontal de un proyectil dependen de su velocidad inicial y su ángulo de proyección.Se obtiene la altura máxima cuando la proyección es vertical hacia arriba 90º y la distancia horizontal máxima cuando el ángulo de proyección es de 45º. | ||
Se puede obtener la misma distancia horizontal, o alcance para dos ángulos de proyección diferentes. Esto es verdad para todos los pares de ángulos que suman 90º. Un objeto lanzado al aire a un ángulo de 30º, por ejemplo, tocará tierra tan lejos como si hubiera sido lanzado a la misma velocidad a un ángulo de 60º. Sin embargo, es obvio que el objeto lanzado a mayor ángulo permanece en el aire más tiempo. | ||
TIRO VERTICAL
La noción de tiro vertical aparece en el campo de la física. Se trata de un movimiento rectilíneo uniforme variado, también conocido como MRUV. En un tiro vertical, la velocidad cambia y existe una aceleración que está dada por la acción de la gravedad.
Puede decirse, de este modo, que el cuerpo lanzado en un tiro vertical sube y luego baja, regresando al punto de partida. Cuando el cuerpo alcanzó la altura máxima, la velocidad resulta nula. En ese instante, el cuerpo deja de subir e inicia su descenso. El tiempo que el cuerpo demora en llegar a la altura máxima resulta idéntico al tiempo que tarda en volver a su punto de partida.
Es importante destacar que existen diversas ecuaciones que permiten medir diferentes magnitudes vinculadas al tiro vertical. Estas ecuaciones trabajan con variables como la velocidad inicial, la altura y la aceleración.
Un ejemplo de tiro vertical se produce cuando tomamos una pelota de tenis con una mano y la lanzamos hacia arriba en línea recta. Dicha pelota subirá durante una breve fracción de tiempo, llegará a su altura máxima y luego descenderá, volviendo a nuestra mano. En la práctica, de todos modos, el tiro vertical puede resultar complicado de realizar ya que el lanzamiento puede no ser recto, el viento puede influir en la pelota, etc.
Lee todo en: Definición de tiro vertical - Qué es, Significado y Concepto http://definicion.de/tiro-vertical/#ixzz48tnMYDdu
Caída libre

Caída libre de una pelota. Se muestran, mediante fotografía estroboscópica, las posiciones de la pelota a intervalos regulares de tiempo: para t = 1, 2, 3, 4, 5, ..., el espacio recorrido es proporcional a 1, 4, 9, 16, 25, ..., etc.
En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también referirse coloquialmente a éstas como caídas libres, aunque los efectos de la viscosidaddel medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como undisparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentaciónalar ni de paracaídas durante un cierto trayecto.1 2
Movimiento rectilíneo uniformemente acelerado

Evolución respecto del tiempo de la posición, de lavelocidad y de la aceleración de un cuerpo sometido a un movimiento rectilíneo uniformemente acelerado, en un sistema de coordenadas cartesianas, según la mecánica clásica.
El movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento rectilíneo uniformemente variado (MRUV), es aquel en el que un móvil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.
Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.
También puede definirse como el movimiento que realiza una partícula que partiendo del reposo es acelerada por una fuerza constante.
El movimiento rectilíneo uniformemente acelerado (MRUA) es un caso particular del movimiento uniformemente acelerado (MUA).
Movimiento rectilíneo uniformemente acelerado en mecánica newtoniana.
En mecánica clásica el movimiento rectilíneo uniformemente acelerado (MRUA) presenta tres características fundamentales:
- La aceleración y la fuerza resultante sobre la partícula son constantes.
- La velocidad varía linealmente respecto del tiempo.
- La posición varía según una relación cuadrática respecto del tiempo.
La figura muestra las relaciones, respecto del tiempo, del desplazamiento (parábola), velocidad (recta con pendiente) y aceleración (constante, recta horizontal) en el caso concreto de la caída libre (con velocidad inicial nula).
El MRUA, como su propio nombre indica, tiene una aceleración constante, cuyas relaciones dinámicas y cinemáticas, respectivamente, son:
(1)
La velocidad v para un instante t dado es:
(2a)
siendo  la velocidad inicial.
la velocidad inicial.
 la velocidad inicial.
la velocidad inicial.
Finalmente la posición x en función del tiempo se expresa por:
(3)
donde 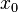 es la posición inicial.
es la posición inicial.
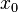 es la posición inicial.
es la posición inicial.
Suscribirse a:
Comentarios (Atom)





