Movimiento rectilíneo uniformemente acelerado
El movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento rectilíneo uniformemente variado (MRUV), es aquel en el que un móvil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.
Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.
También puede definirse como el movimiento que realiza una partícula que partiendo del reposo es acelerada por una fuerza constante.
El movimiento rectilíneo uniformemente acelerado (MRUA) es un caso particular del movimiento uniformemente acelerado (MUA).
Movimiento rectilíneo uniformemente acelerado en mecánica newtoniana.
En mecánica clásica el movimiento rectilíneo uniformemente acelerado (MRUA) presenta tres características fundamentales:
- La aceleración y la fuerza resultante sobre la partícula son constantes.
- La velocidad varía linealmente respecto del tiempo.
- La posición varía según una relación cuadrática respecto del tiempo.
La figura muestra las relaciones, respecto del tiempo, del desplazamiento (parábola), velocidad (recta con pendiente) y aceleración (constante, recta horizontal) en el caso concreto de la caída libre (con velocidad inicial nula).
El MRUA, como su propio nombre indica, tiene una aceleración constante, cuyas relaciones dinámicas y cinemáticas, respectivamente, son:
(1)
La velocidad v para un instante t dado es:
(2a)
siendo  la velocidad inicial.
la velocidad inicial.
 la velocidad inicial.
la velocidad inicial.
Finalmente la posición x en función del tiempo se expresa por:
(3)
donde 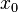 es la posición inicial.
es la posición inicial.
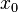 es la posición inicial.
es la posición inicial.




No hay comentarios.:
Publicar un comentario